|
Phase and TV Based Convex Sets for
Blind Deconvolution for Microscopic Images
In
this article, two closed and convex sets for blind deconvolution
problem are proposed. Most blurring functions in microscopy are
symmetric with respect to the origin. Therefore, they do not modify the
phase of the Fourier transform (FT) of the original image. As a result
blurred image and the original image have the same FT phase. Therefore,
the set of images with a prescribed FT phase can be used as a
constraint set in blind deconvolution problems. Another convex set that
can be used during the image reconstruction process is the Epigraph Set
of Total Variation (ESTV) function. This set does not need a prescribed
upper bound on the total variation of the image. The upper bound is
automatically adjusted according to the current image of the
restoration process. Both of these two closed and convex sets can be
used as a part of any blind deconvolution algorithm. Simulation
examples are presented.
The preprint version of the paper can be dowloaded from here.
The blind
deconvolution software for the proposed algorithm is here.
The blind
deconvolution software for the Lucy Richardson's algorithm is here.
The PES-TV
denoising software is available here.
The paper
including the results for Lucy-Richardson's algorithm is
available here.
An example of
blind deconvolution using two different deblurring methods. The
original image is blurred by a Gaussian with σ = 5. The reconstruction results are presented in (c),
and (d):
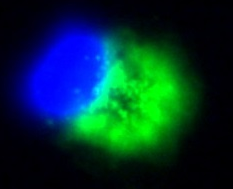
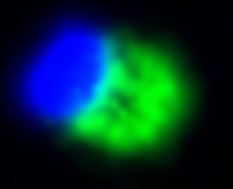
(a) Original
Image
(b) Blurred Image
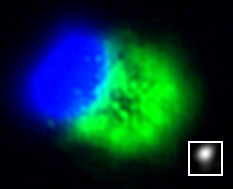
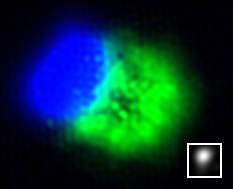
(c) Ayers-Phase-ESTV-based method
(d)
Ayers method
Our method which
incorporates phase information and TV constraint produces better
results than the ordinary Ayers method.
An example of
blind deconvolution using two different deblurring methods. The
original image is blurred by a Gaussian with σ = 3. The reconstruction results are presented in (c),
and (d):
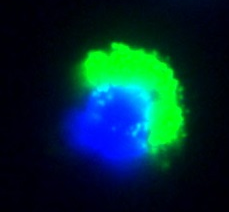

(a) Original
Image
(b) Blurred Image
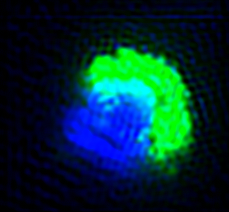

(c) Ayers-Phase-ESTV-based method
(b)
Ayers method
Our method which
incorporates phase information and TV constraint produces better
results than the ordinary Ayers method (which does not converge).
The blind
deconvolution results using proposed method and Ayers method for
blurring Gaussian PSFs with σ = 3 and σ = 7 are presented here.
Another simulation example is presented here. Image (b) in this pdf file is
obtained using this code.
|