Phase and TV Based Convex Sets for Blind Deconvolution of Microscopic Images

Most blurring kernels encountered in real life are symmetric therefore they do not alter the phase of the Fourier transform (FT) of the original image. The presented algoritm uses this fact combined with a Epigraph Set of Total Variation (ESTV) constraint to solve the blind deconvolution problem in a effective manner. The capabilities of the algoritm are illustared on microscopic image examples. <

We provide our matlab implementation of the algorihtm at

• Phase and TV Based Convex Sets for Blind Deconvolutionin MATLAB,
• Complete description of the codes is available in the following link: Phase and TV Based Convex Sets for Blind Deconvolution

This paper is under revision at IEEE Journal of Selected Topics - Advanced Signal Processing in Microscopy and Cell Imaging.

Phase and TV Based Convex Sets for Blind Deconvolution

The algorihtm is composed of a loop between two convex constraints that are solved sequentially in an iterative manner. The block diagram of the algorithmic loop is as below

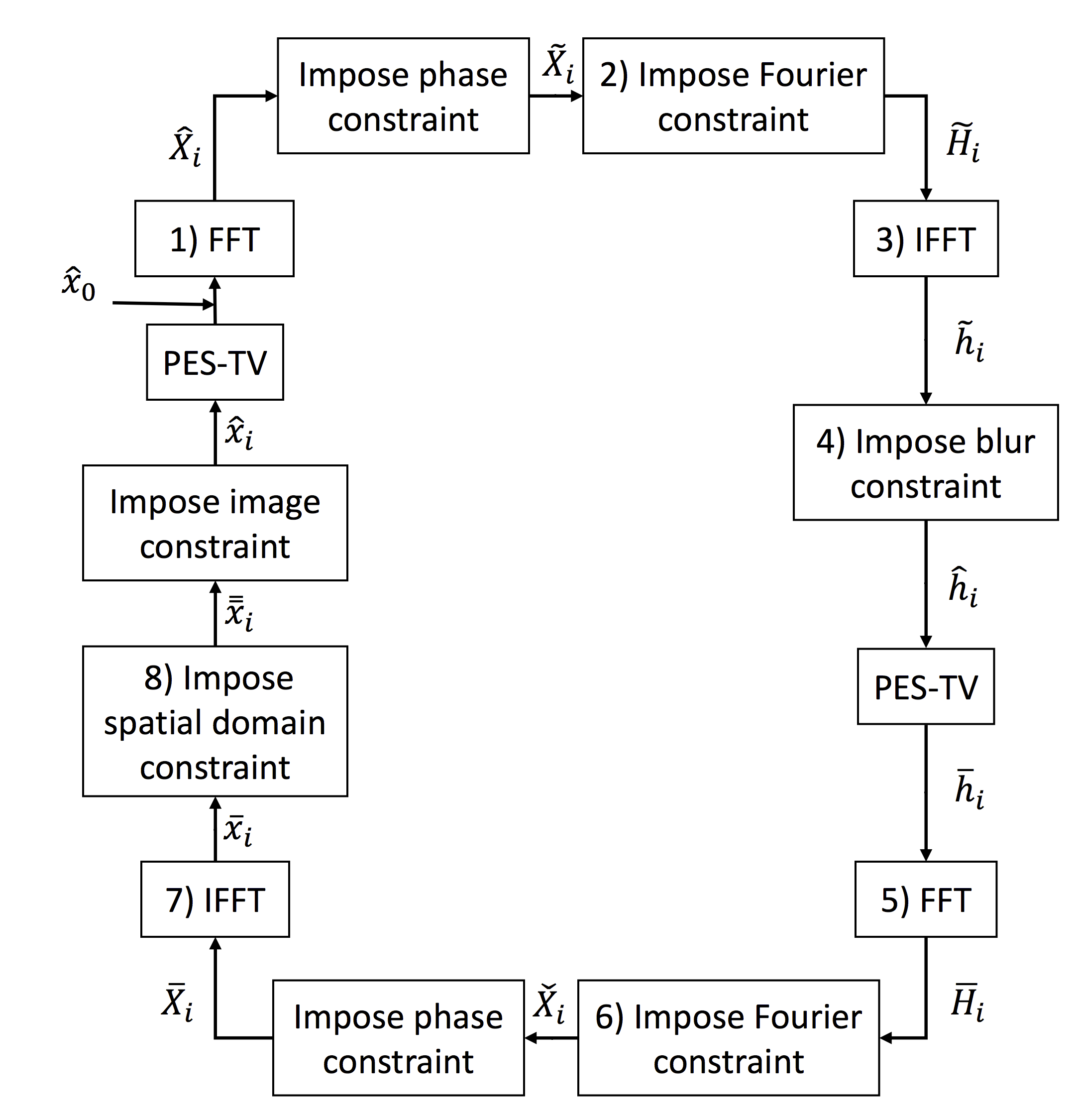
In the following parts of the page, we present a set of examplar blind deconvolution results using the proposed blind deconvolution method. We also provide comparisons with other blind deconvlution algorihtms from the literature.

Tests of the proposed algorithm on a natural image.

We use below image in (a) that is taken from [1], and compare our algorihtm agains the method agains the results presented in [1] and [2]

Fig. 2 The Gaussian blurred version of image (with σ = 6 and PSNR = 24.05 dB) in (b) is reconstructed using various methods. In (c) the image is deblurred using the non-blind deconvolution method in [47] (PSNR = 22.43 dB). In (d) the result of the Ayers-Dainty algorithm is presented (PSNR = 24.86 dB). In (e) and (f) we present the result of the Ayers-Dainty together with phase constraint (PSNR = 24.91 dB) and Ayers-Dainty and ESTV projection (PSNR = 24.74 dB), respectively. (g) Ayers-Dainty with phase and ESTV projections (PSNR = 25.18 dB). This is a sharp image but there are some ringing artifacts. (h) The restoration result of the non-blind approach based on phase only iterations (PSNR = 24.58 dB). This is the only image clearly showing the white cable or stripe on the ground and the two antennas are clearly visible.

Simulation results with Immunofluorescense images of CD133 positive Huh7 liver cancer cells

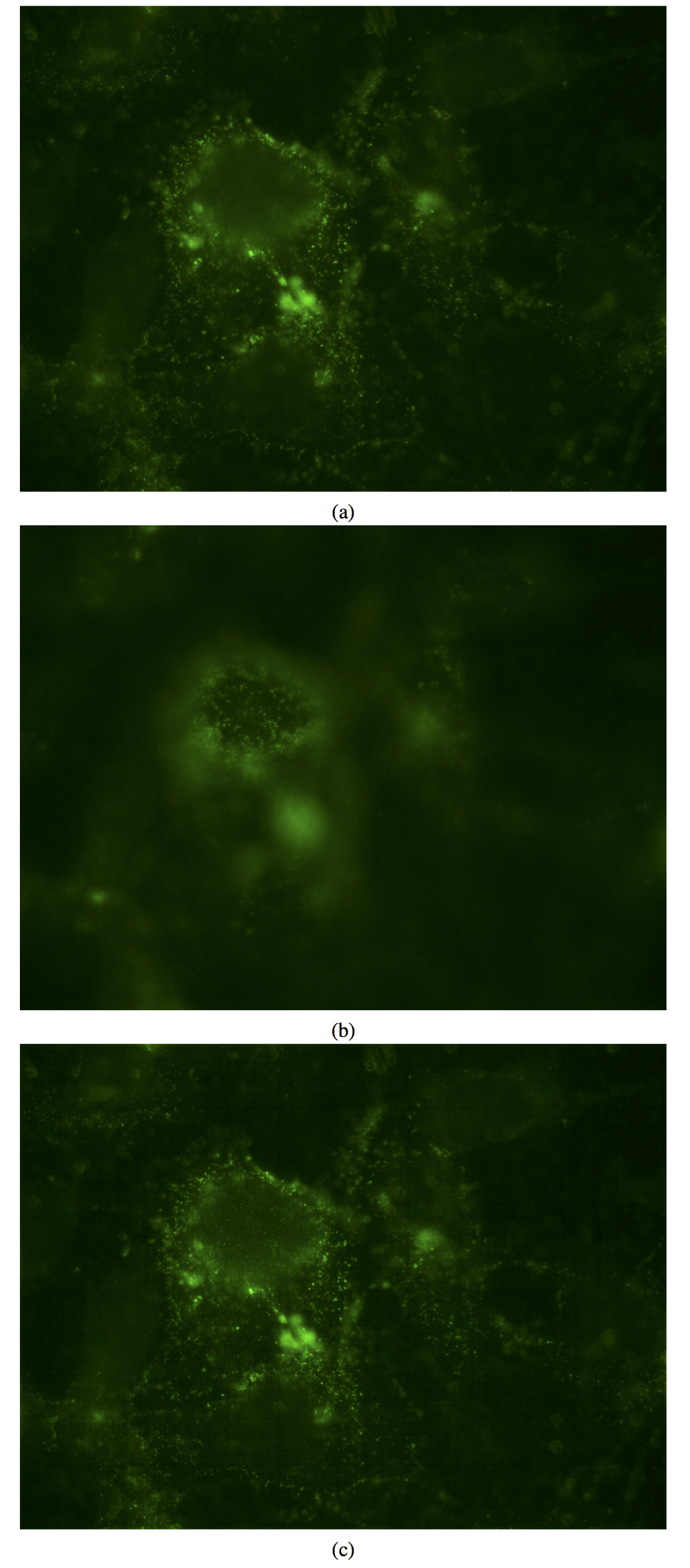
Fig. 3 Immunofluorescense images of CD133 positive Huh7 liver cancer cells with differential focus: (a) xf (top), (b) xg (middle). The images xf and xg are combined to obtain (c) the deblurred image using Gaussian filtering based edge- enhancement together with phase and ESTV projections.

We have extensively tested the algorithm on various Fluoresence microscopy images and compared our results against other methods in the literature

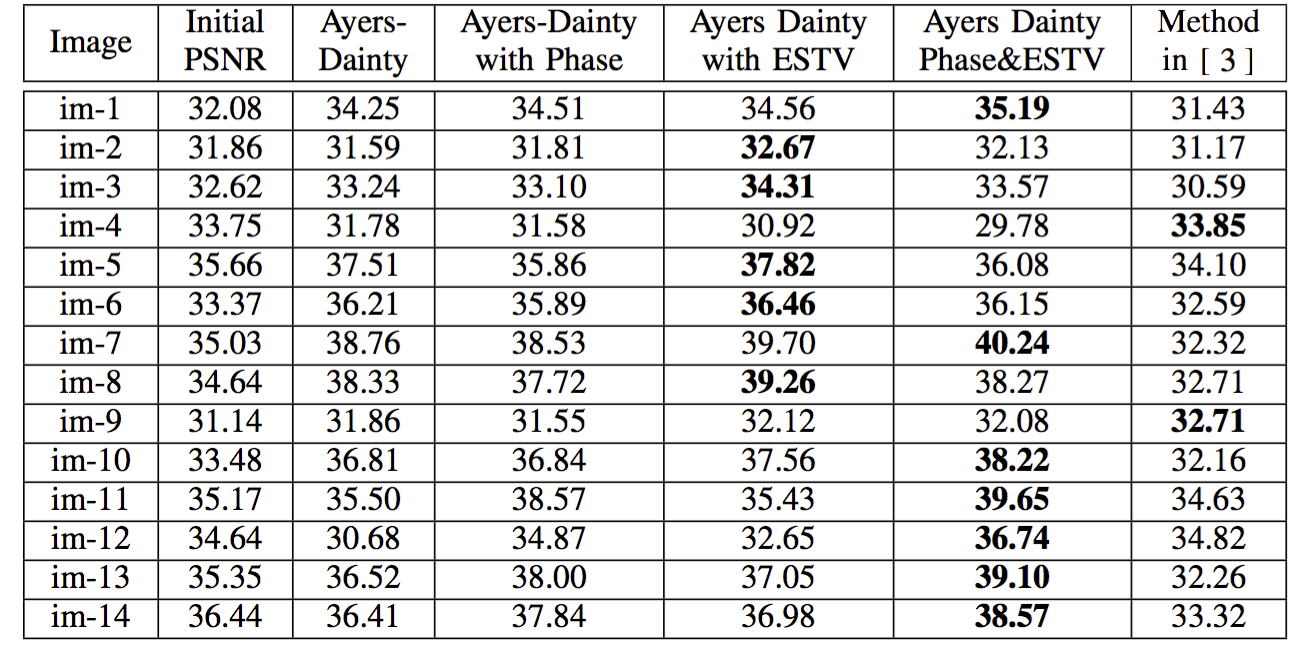
Table 1. Deconvolution results for FL microscopic images blurred by a Gaussian filter with disc size 20 and σ = 5. PSNR (dB) values are reported.

Bibliography