Bilkent University
Bilkent EEE Department
 BilSPG
A. Enis Cetin
Mohammad Tofighi

Denosing Using Wavelets and Projections onto the L1-Ball

L1-ball denoising software provides examples of denoising using projection onto the epigraph of L1-ball (PES-L1). Description of each file is given in the related mfile. Moreover, you can find complete explanation of the PES-L1 algorithm and the codes in the given pdf below. Please feel free to contact us if you had any question.

This paper is published in IEEE Signal Processing Magazine which you can find it here.

Denoising using Projection onto Epigraph Set of L1-ball (PES-L1):

Considering the following signal:

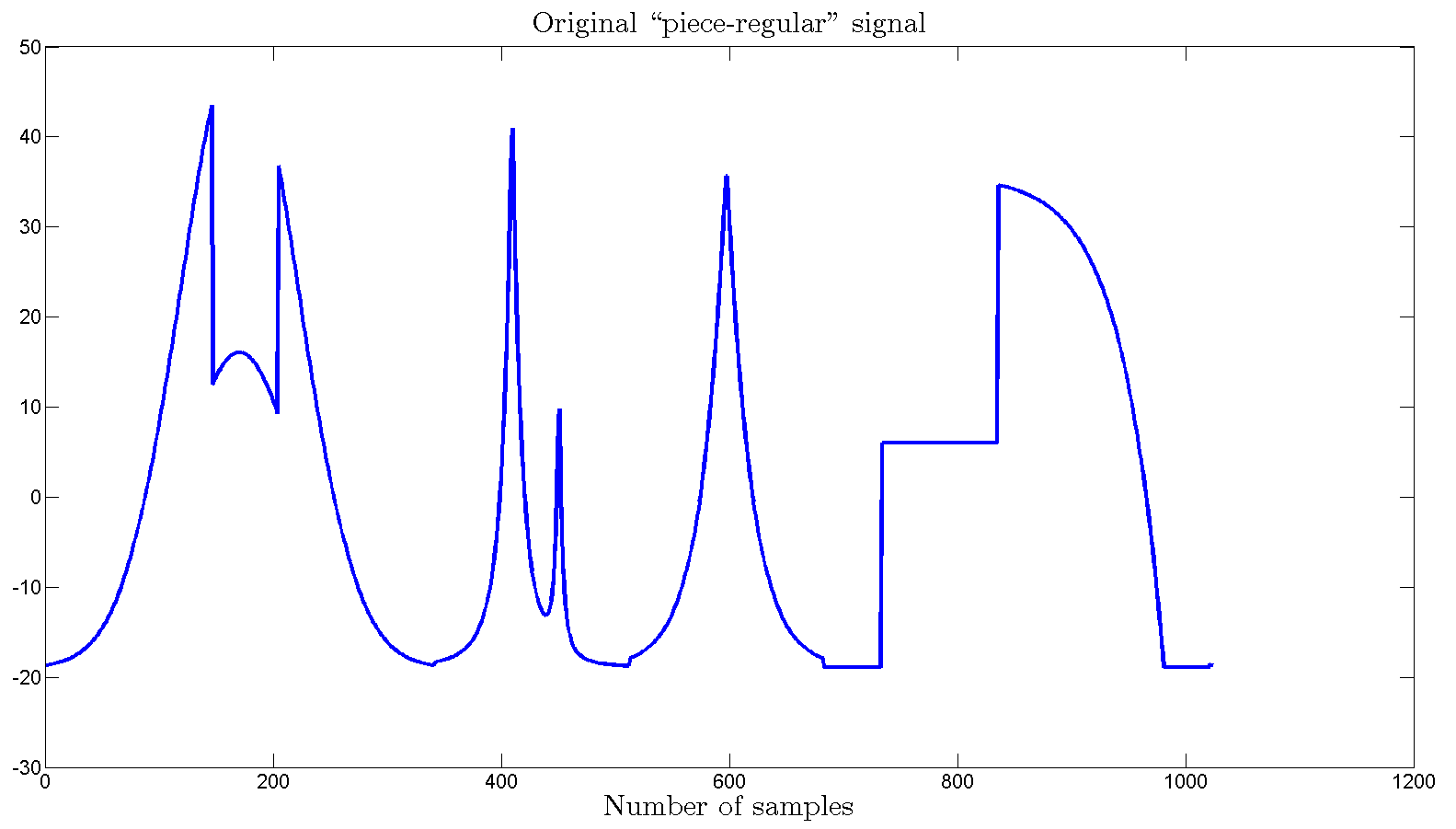
Fig. 1

This signal is corrupted with additive, i.i.d. Gaussian noise with zero mean (ξ [n]) as x[n] = v[n] + ξ[n], which v[n] is the original discrete-time signal and x[n] is the noisy version of v[n],which has standard deviation equal to 10% of the maximum amplitude of the original signal, which is shown below:

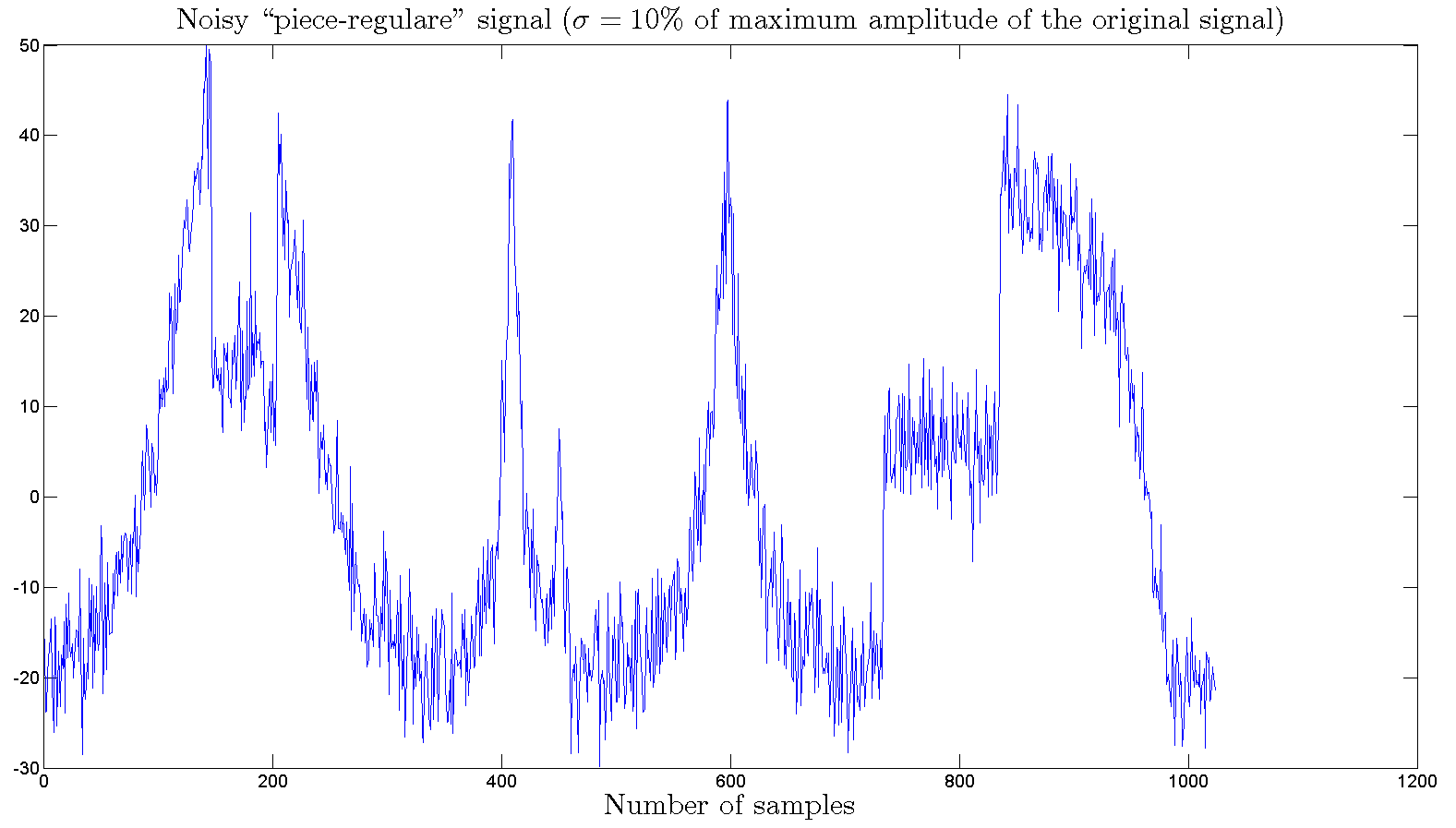
Fig. 2

PES-L1 using pyramidal structure:

PES-L1 ball denoising is applied according to the followoing block-diagram:

Fig. 3

The noisy signal is low-pass filtered with cut-off frequency π/8 for "piece-regular" signal and the output xlp[n] is subtracted from the noisy signal x[n] to obtain the high-pass signal xhp[n] as shown in Fig. 3. The signal is projected onto the epigraph of L1-ball and xhd[n] is obtained. Projection onto the Epigraph Set of L1-ball (PES-L1), removes the noise by soft-thresholding. The denoised signal xden[n] is reconstructed by adding xhd[n] and xlp[n] as shown in Fig. 3. Since the soft-thresholding is a nonlinear operation, it may be advantages to iterate or circulate the signal several times in the pyramidal structure as in wavelet denoising. A low-pass filter with cut-off π/4 is used in pyramidal structure.


And the resulting denoised signal, using this code PES_L1_Pyramid_Denoising, is as follows:

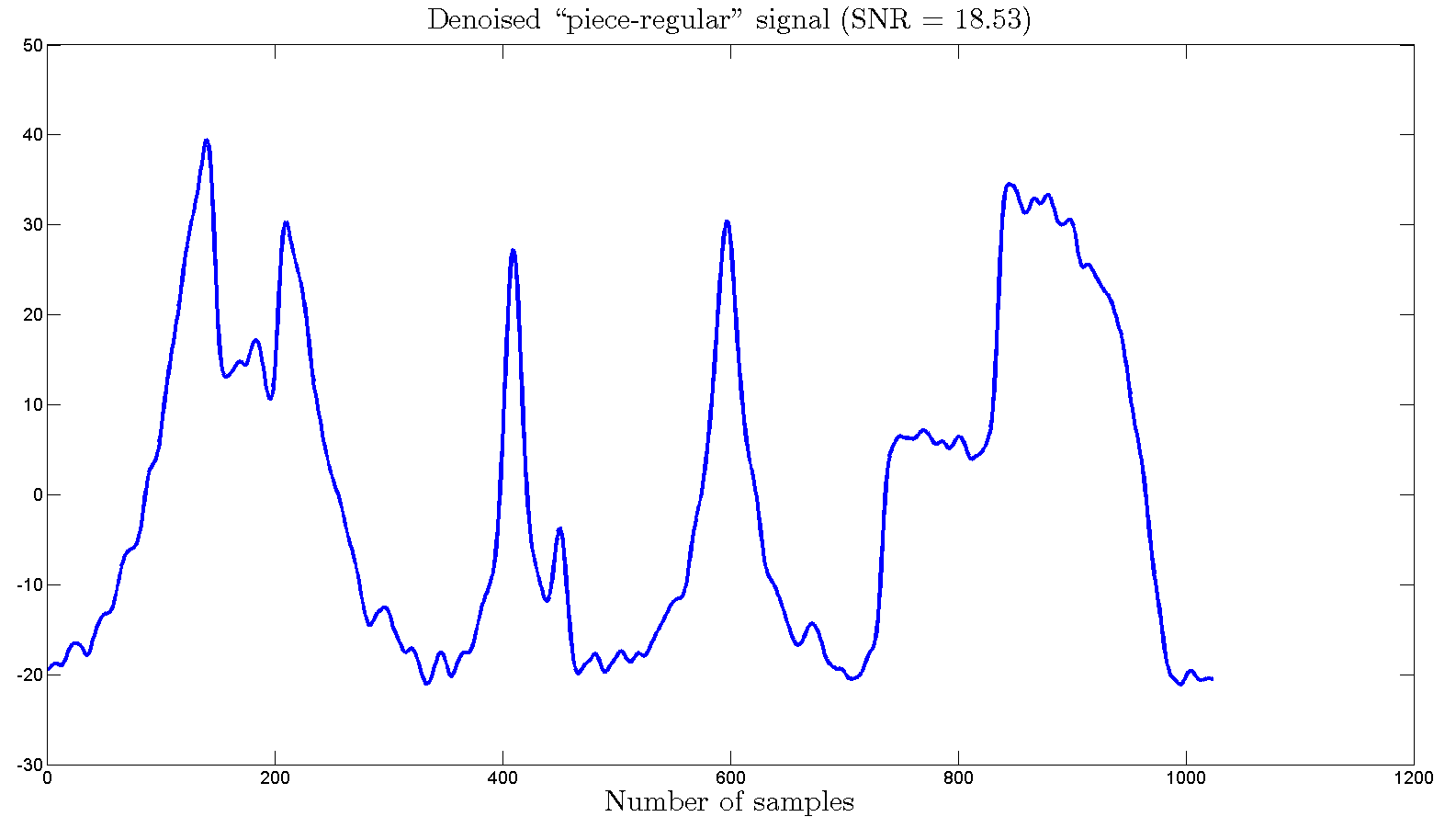
Fig. 4

PES-L1 using wavelet decomposition:

In denoising using PES-L1 with wavelet decomposition the It is possible to use the Fourier transform of the noisy signal to estimate the bandwidth of the signal. Once the bandwidth ω0 of the original signal is approximately determined it can be used to estimate the number of wavelet transform levels and the bandwidth of the low-band signal xL . In an L-level wavelet decomposition the low-band signal xL approximately comes from the [0, π/2L] frequency band of the signal x[n] . Therefore, π/2L must be greater than ω0 so that the actual signal components are not soft-thresholded. Only wavelet subsignals wL[n] , wL-1[n] , … , w1[n] which come from frequency bands [π/2L, π/2L-1] , [π/2 L-1, π/2L-2] , ..., [π/2, π] , respectively, should be soft-thresholded in denoising. For example, in Fig. 5, the magnitude of Fourier transform of x[n] is shown for "piece-regular" signal defined in MATLAB. This signal is corrupted by white Gaussian noise with σ = 10, 20, 30 %  of the maximum amplitude of the original signal. For this signal a L=3 level wavelet decomposition is suitable because Fourier transform magnitude approaches to the noise floor level after ω0 = 58π/512 . It is also a good practice to allow a margin for signal harmonics. Therefore, L=3 (π/8> ω0 ) is selected as the number of wavelet decomposition levels.

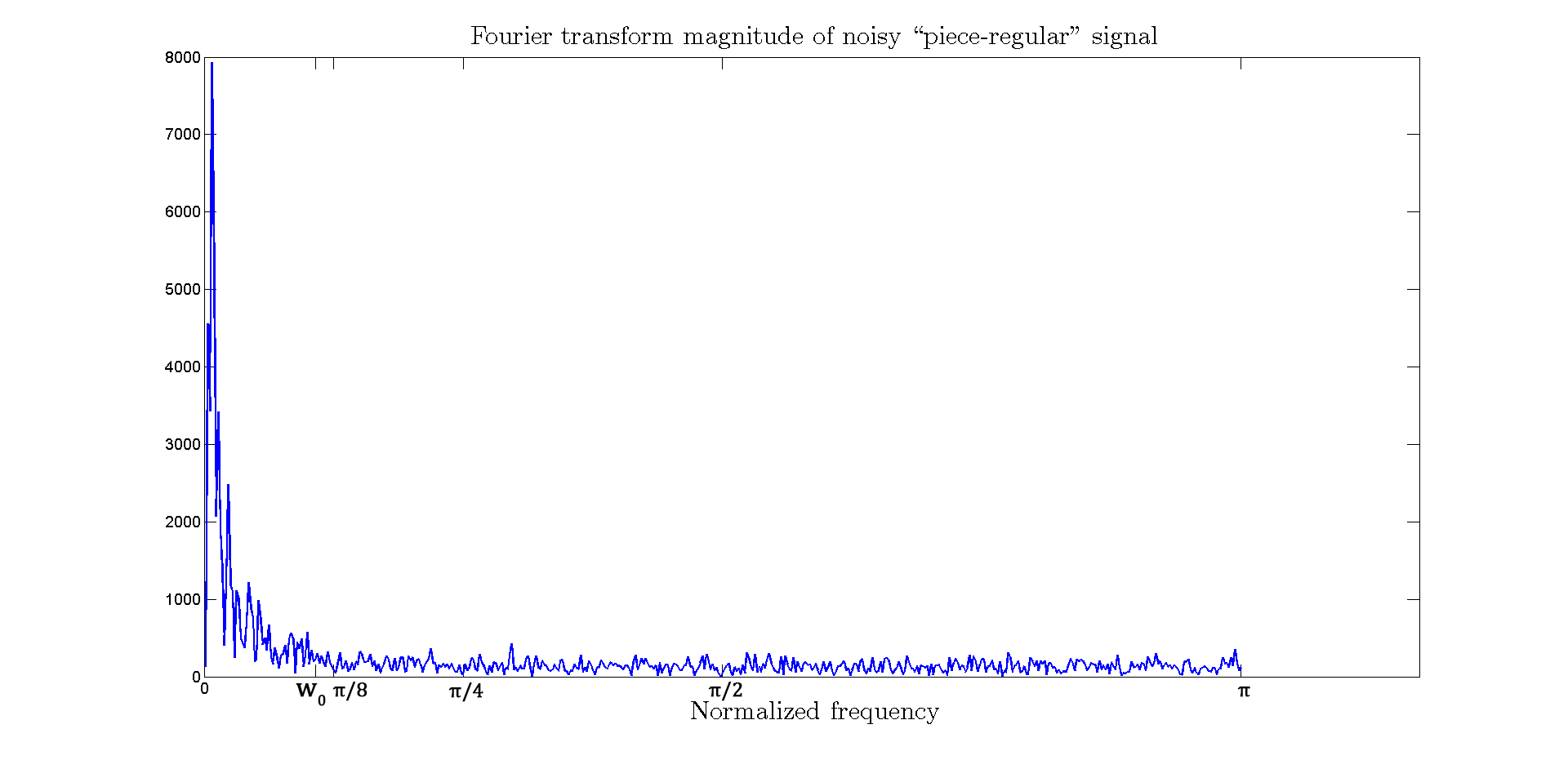
Fig. 5

Epigraph set based threshold selection is compared with wavelet denoising methods used in MATLAB [2, 3, 4, 5]. The "piece-regular" signal shown in Fig. 1 is corrupted by a zero mean Gaussian noise with σ = 10 %  of the maximum amplitude of the original signal. The signal is restored using PES-L1 with pyramid structure, PES-L1 with wavelet, MATLAB's wavelet multivariate denoising algorithm [3, 4], MATLAB's soft-thresholding denoising algorithm, and Peyre's denoising method. The denoised signals using PES-L1 with pyramid structure, PES-L1 with wavelet are shown in Fig. 4, and 6, with SNR values equal to 18.53, 18.05, respectively. Results for other test signals in MATLAB are presented in Tables in the paper above. These results are obtained by averaging the SNR values after repeating the simulations for 300 times. The SNR is calculated using: SNR = 20×log10( ||worig || / ||worig - wrec || ) . 

The denoised "piece-regular" signal with PES-L1 using wavelet decomposition is as follows:



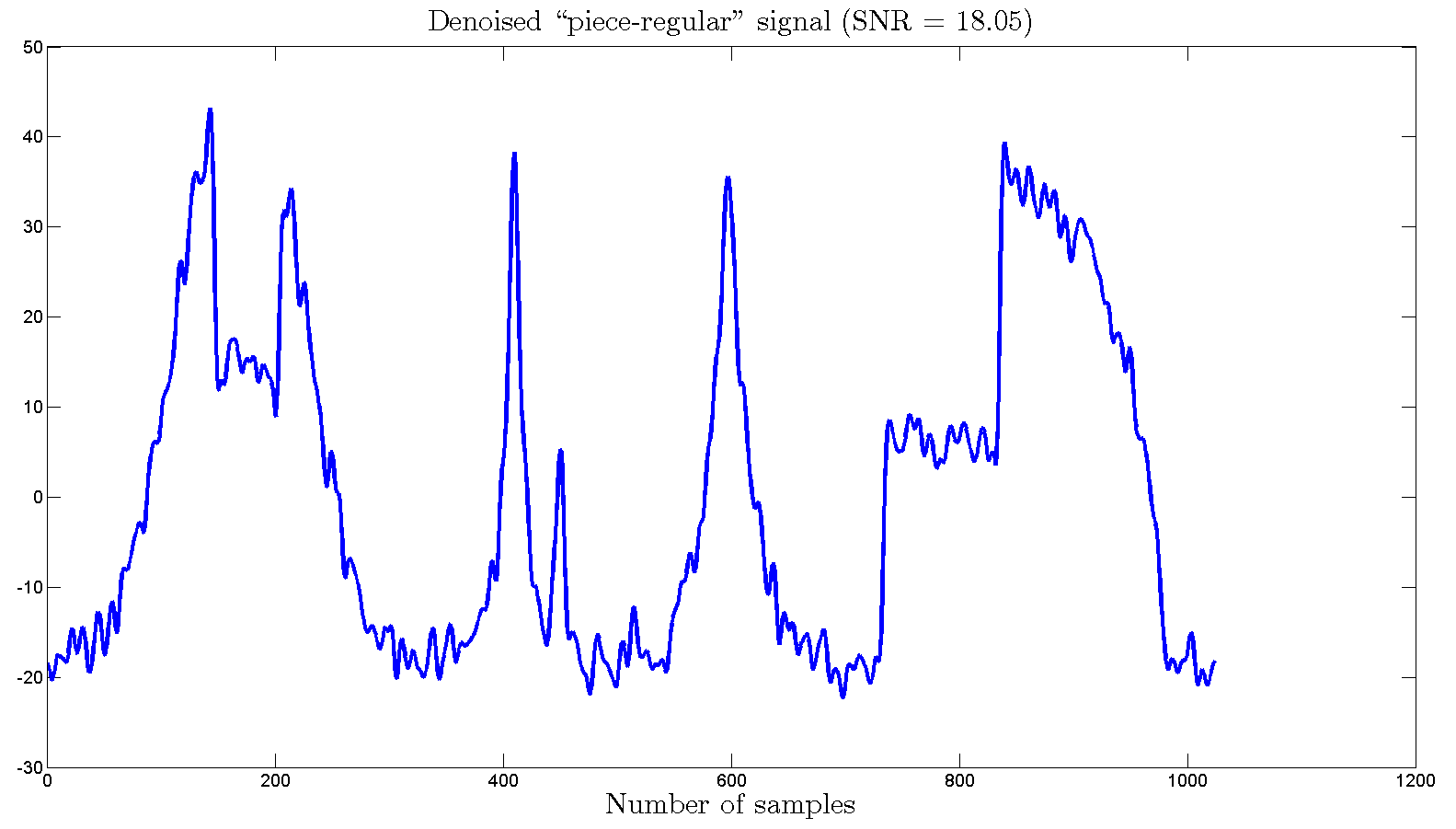
Fig. 6

Bibliography

[1] S. Mallat and W.-L. Hwang, “Singularity detection and processing with wavelets,” Information Theory, IEEE Transactions on, vol. 38, no. 2, pp. 617–643, Mar 1992.
[2] D. Donoho, “De-noising by soft-thresholding,” Information Theory, IEEE Transactions on, vol. 41, no. 3, pp. 613–627, May 1995.
[3] M. Aminghafari, N. Cheze, and J.-M. Poggi, “Multivariate denoising using wavelets and principal component analysis,” Computational Statistics and Data Analysis, vol. 50, no. 9, pp. 2381 – 2398, 2006.
[4] P. J. Rousseeuw and K. V. Driessen, “A fast algorithm for the minimum covariance determinant estimator,” Technometrics, vol. 41, no. 3, pp. 212–223, 1999.
[5] S. Chang, B. Yu, and M. Vetterli, “Adaptive wavelet thresholding for image denoising and compression,” IEEE Transactions on Image Processing, vol. 9, no. 9, pp. 1532–1546, Sep 2000.
[6] D. L. Donoho and I. M. Johnstone, “Adapting to unknown smoothness via wavelet shrinkage,” Journal of the American Statistical Association, vol. 90, no. 432, pp. 1200–1224, 1995. [Online]. Available: http://amstat.tandfonline.com/doi/abs/10.1080/01621459.1995.10476626
[7] G. Chierchia, N. Pustelnik, J.-C. Pesquet, and B. Pesquet-Popescu, “An epigraphical convex optimization approach for multicomponent image restoration using non-local structure tensor,” in IEEE ICASSP, 2013, 2013, pp. 1359–1363.
[8] A. E. Cetin, A. Bozkurt, O. Gunay, Y. H. Habiboglu, K. Kose, I. Onaran, R. A. Sevimli, and M. Tofighi, “Projections onto convex sets (POCS) based optimization by lifting,” IEEE GlobalSIP, Austin, Texas, USA, 2013.
[9] K. Kose, V. Cevher, and A. Cetin, “Filtered variation method for denoising and sparse signal processing,” in 2012 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), March 2012, pp. 3329–3332.
[10] G. Chierchia, N. Pustelnik, J.-C. Pesquet, and B. Pesquet-Popescu, “Epigraphical projection and proximal tools for solving constrained convex optimization problems: Part i,” Arxiv, CoRR, vol. abs/1210.5844, 2012.
[11] J. Duchi, S. Shalev-Shwartz, Y. Singer, and T. Chandra, “Efficient projections onto the l1-ball for learning in high dimensions,” in Proceedings of the 25th International Conference on Machine Learning, ser. ICML ’08. New York, NY, USA: ACM, 2008, pp. 272–279.
[12] R. Baraniuk, “Compressive sensing [lecture notes],” IEEE Signal Processing Magazine, vol. 24, no. 4, pp. 118–121, 2007.
[13] J. Fowler, “The redundant discrete wavelet transform and additive noise,” Signal Processing Letters, IEEE, vol. 12, no. 9, pp. 629–632, Sept 2005.